令和4年度上期 電験三種【理論】を解いてみた(感想と解き方のコツ)
令和4年度上期 電験三種【理論】を解いてみた
電験の知識を錆び付かせないために、令和4年度上期 電験三種【理論】を解いて見ました。
ちなみに、私は令和3年度電験二種試験に合格しています。
しかも、Twitter等のうわさでは「令和4年度上期 電験三種【理論】科目」はそこまで難しくないとのことです。
理論科目は計算問題が中心のため、「運」で合格できる要素が少ない科目です。ブランクが大きいので、6割は取れないかもしれないな…。と、弱気ですが、過去の知識の遺産と、勘で当てる方法を駆使して、何点取れるのかやってみたいと思います。
結果は…
85点でした!
超高得点のため、非常に嬉しいですが、実は勘で3問当てています。でもまあ、運も実力のうちということで…。
自信ありで正解:問2、4、5、8、12、15(a)、16(a)、16(b)、17(a)、17(b)
自信なしで正解:問3、6、7、9、11、14、15(b)
不正解:問1、10、13
解いて見ての感想ですが、確かに難問は少なく、基本的な問題が中心でした。さっぱり分からなかったのは問13ぐらいであり、しっかり過去問を中心に勉強された方なら、合格できそうな内容でした。
私自身、基本的な問題の解き方をかなり忘れていたため、「定期的な復習が大切だな」と感じている次第であります。
参考に、私の解き方・考え方を紹介させていただきます。私が思う難易度も評価してみました。間違っているところがあるかもしれませんこと、ご了承ください。(もし、間違いがありましたら、コメント等もらえると大変ありがたいです)
令和4年度上期 電験三種 理論科目

【正解の答え】問1:(3) 難易度:
私の結果 ⇒ 不正解(1)
【考え方】
あれ、誤りの選択肢が無いなあ。分からないなあ。ということで(1)を選択しましたが不正解でした。
正解は(3)ですが、E[V/m]=V[V]/d[m]なので、電界の大きさは誘電率と関係無かったです。この問題を落としたのはショック…。
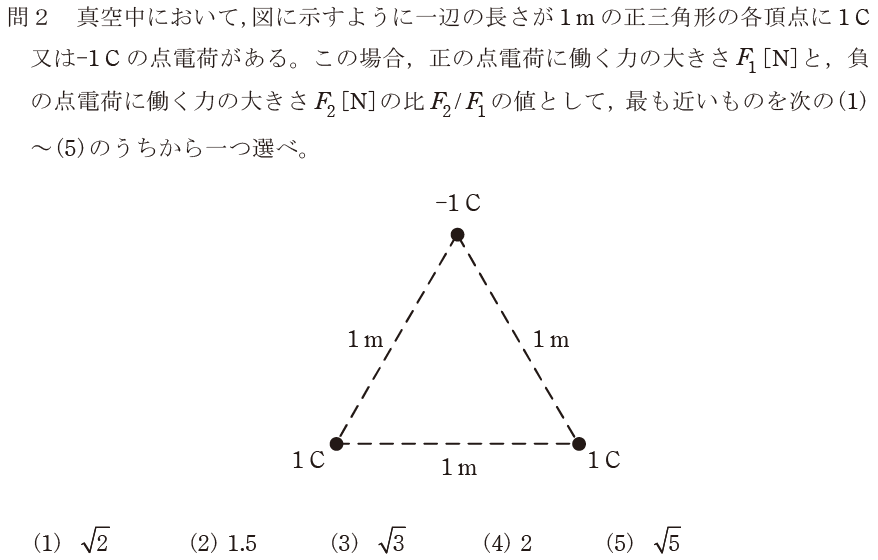
【正解の答え】問2:(3) 難易度:
私の結果 ⇒ 正解
【考え方】
点電荷に働く力を求める基本的な問題です。(3)を選択し、正解でした。
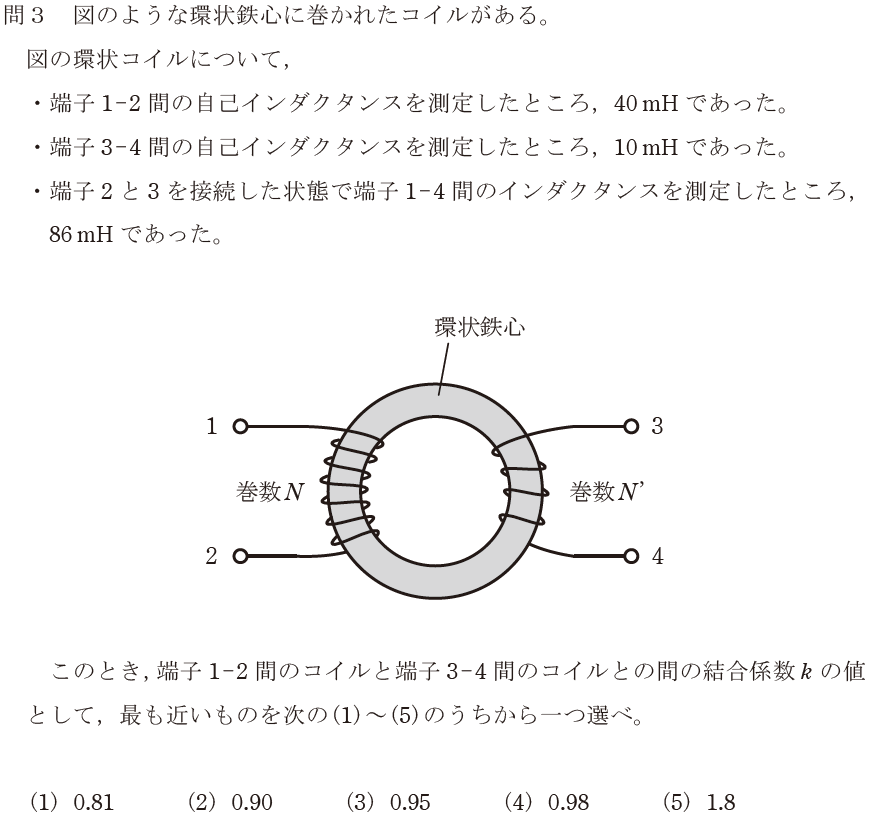
【正解の答え】問3:(2) 難易度:
私の結果 ⇒ 正解
【考え方】
わ、分からん…。というわけで、実力での回答を放棄し、勘で当てる作戦に切り替えます。(5)の選択肢が「1.8」であり、一つだけ他の選択肢とかけ離れた数字であったため、この選択肢は間違いだろう。
この明らかに間違いであろう「1.8」と共通項を持つ選択肢を探したところ、(2)が「0.9(※1.8÷2)」であったため、(2)を選択したところ正解でした。
このように、明らかに間違いの選択肢と共通項を持つ選択肢(例えば、×2とか、÷2した値)は、正解の可能性が高いように思います。
この問題を実力で正解する場合、相互インダクタンスM=k√(L12×L34)、和動接続の合成インダクタンスL=L12+L34+2Mの公式を覚えている必要があります。私は和動接続の合成インダクタンスを忘れていたため、実力で解くことができませんでした。
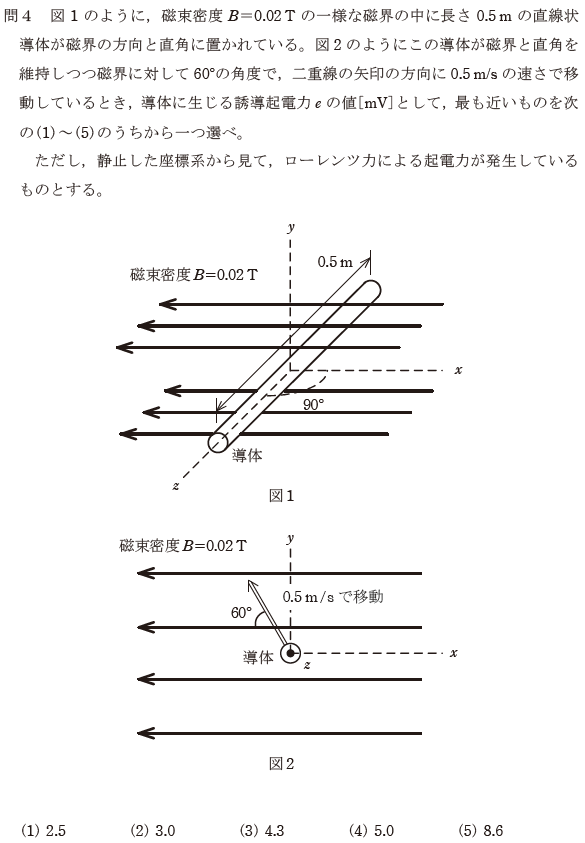
【正解の答え】問4:(3) 難易度:
私の結果 ⇒ 正解
【考え方】
これも典型的な誘導起電力を求める問題です。60°の角度が付いているのがほんの少しいやらしい程度です。(3)を選択して正解でした。
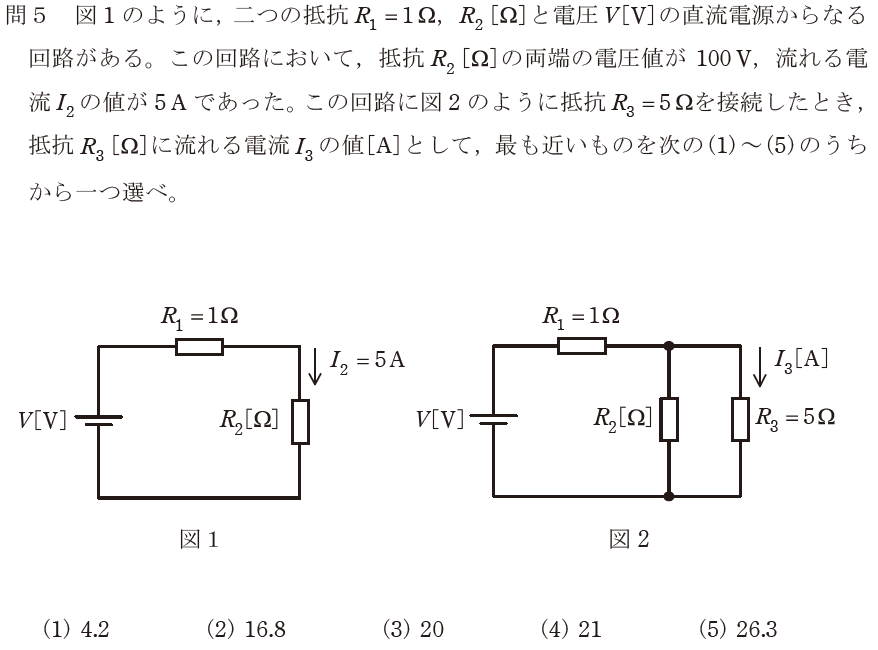
【正解の答え】問5:(2) 難易度:
私の結果 ⇒ 正解
【考え方】
これも典型的な直流回路における抵抗に流れる電流を求める問題です。(2)を選択して正解でした。
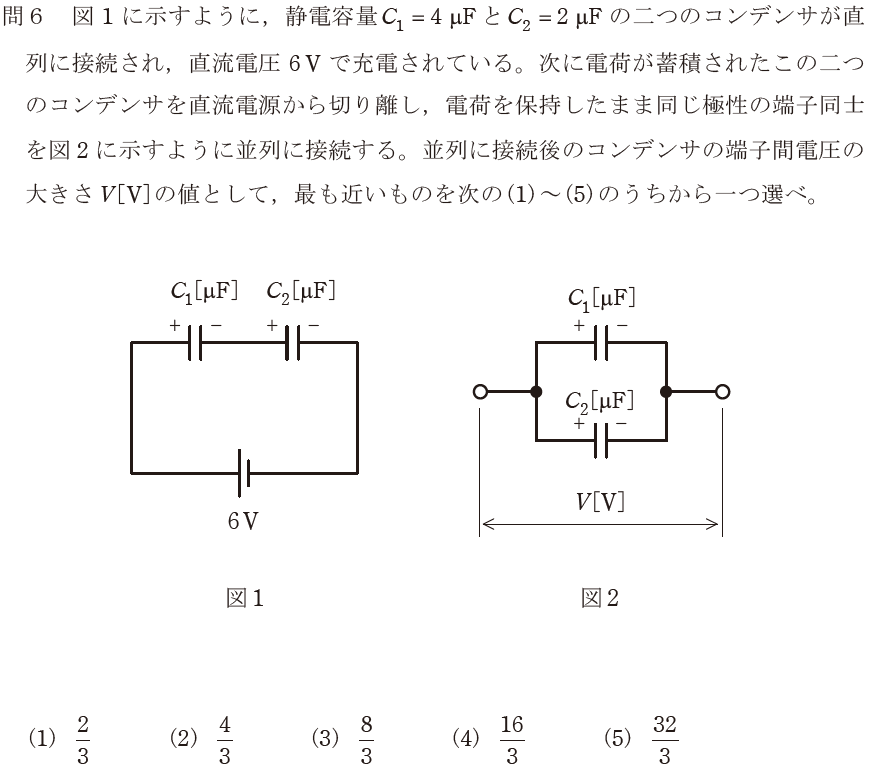
【正解の答え】問6:(3) 難易度:
私の結果 ⇒ 正解
【考え方】
直列・並列のコンデンサについての問題です。電荷、コンデンサ容量、電圧の計算方法がごっちゃごちゃになってしまい混乱してしまいますが(私だけ?)、落ち着いて計算しましょう。(3)を選択して正解でした。
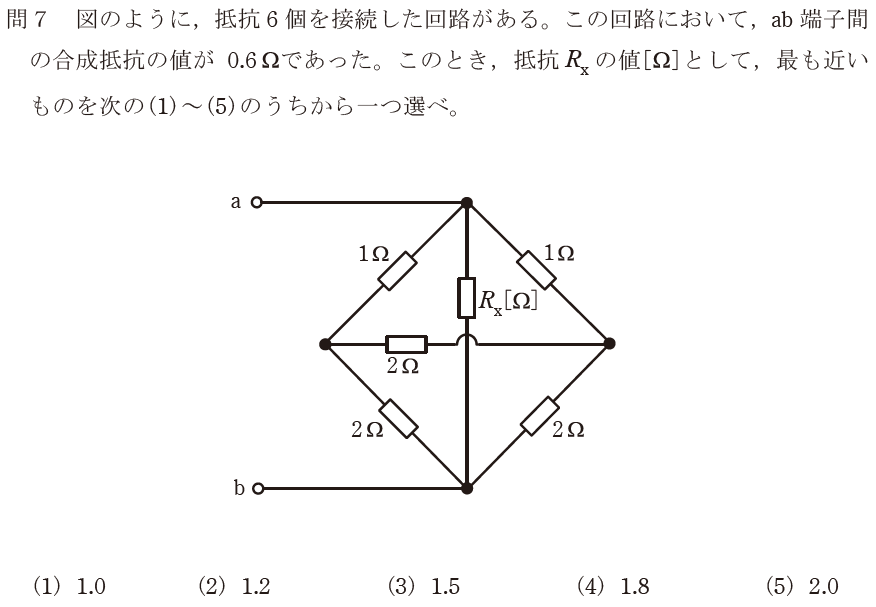
【正解の答え】問7:(1) 難易度:
私の結果 ⇒ 正解
【考え方】
一見難しいですが、よくよく見ると真ん中の2Ωの抵抗には電流が流れてないことが分かります。これを発見できれば、合成抵抗を求めるだけの簡単な問題となります。(1)を選択して正解でした。
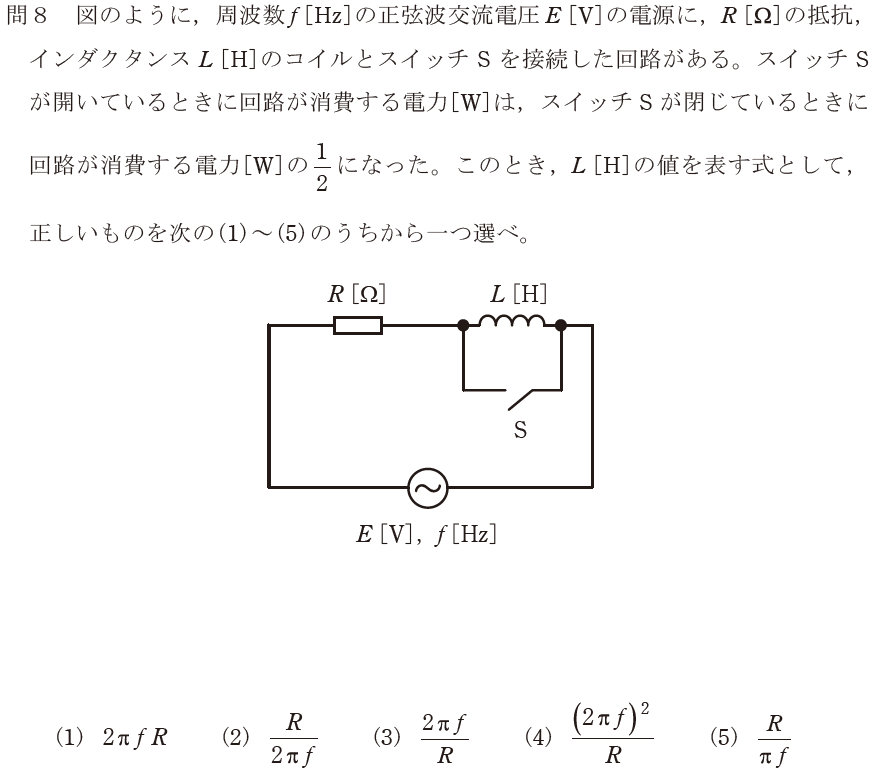
【正解の答え】問8:(2) 難易度:
私の結果 ⇒ 正解
【考え方】
つまり、R[Ω]と、L[H]のリアクタンス「2πf×L」[Ω]が等しいということが発見できれば、R=2πf×Lより、(2)を選択して正解でした。
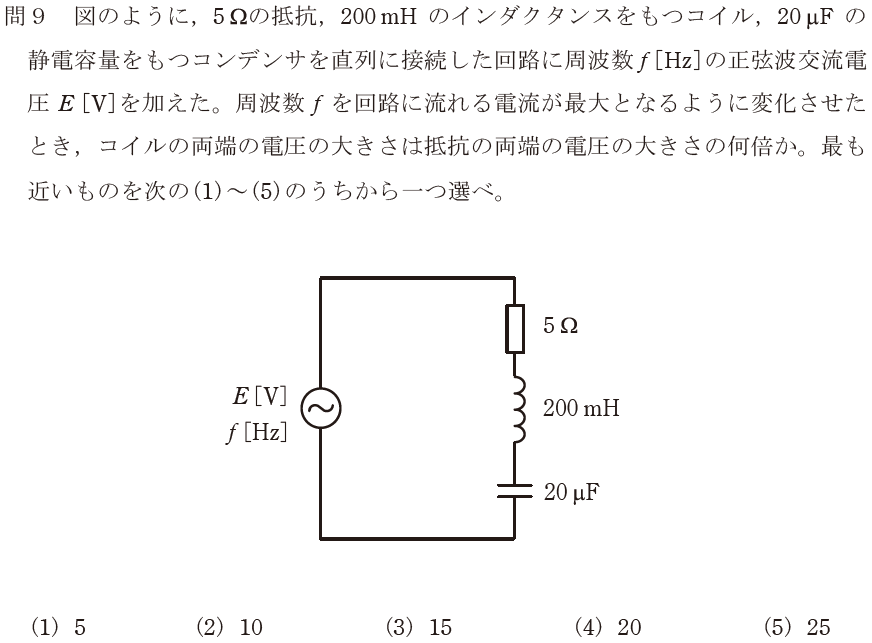
【正解の答え】問9:(4) 難易度:
私の結果 ⇒ 正解
【考え方】
直列回路の共振に関する問題ですが、すっかり忘れていたため、勘で回答を選ぶしかない。
計算問題において(1)と(5)は正解になり難いし、きれいな数字が正解になりやすいから、(2)「10」または(4)「20」のどちらかが正解だろう。コイルの0.2[Ω]に対して、抵抗の5[Ω]は25倍だから、(4)の「20」が正解では?という全く根拠のない謎論理により、(4)を選択したところ正解でした。
実力で解く場合、「直列共振において、回路のインピーダンスZは最小となり、流れる電流は最大となる」、「共振周波数f0=1/(2π√(LC))[Hz]」により、共振時のコイルのリアクタンスを求め、コイルに流れる電圧を計算する必要があります。
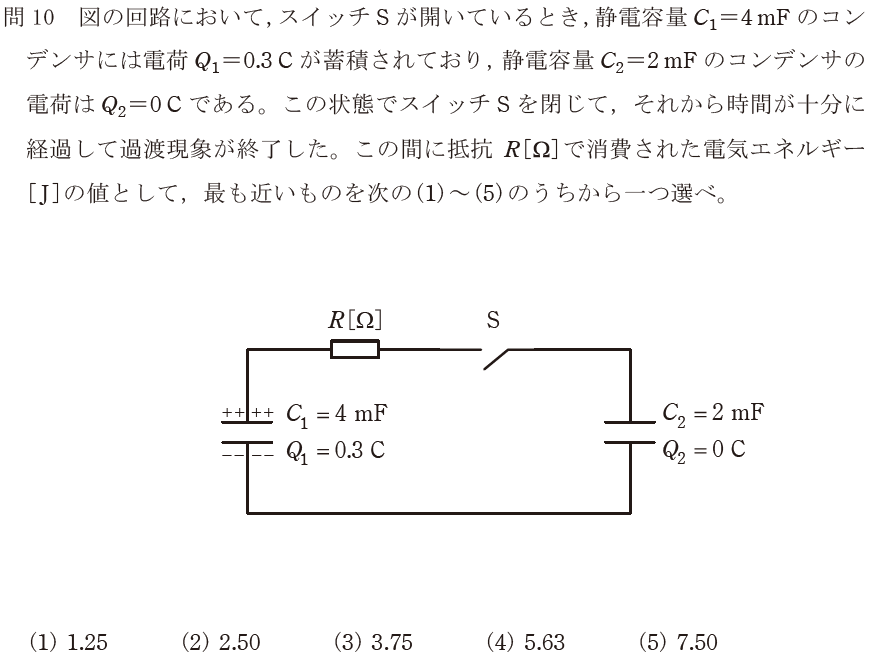
【正解の答え】問10:(3) 難易度:
私の結果 ⇒ 不正解(2)
【考え方】
これまた解き方が分からない…。
V1が75[V]、Q1+Q2が0.3[Q]なのだから、(2)「2.50」[J]ぐらいが正解では?ということで(2)を選択して不正解でした。
正攻法で解く場合、まずはC1に蓄えられている静電エネルギーを求め、次にスイッチを閉じた後の電圧を求め(両方のコンデンサにかかる電圧は等しい)、C1及びC2の静電エネルギーを求めて合計し、「スイッチを閉じる前の静電エネルギ」ー「C1とC2の静電エネルギーの合計値」を計算することで、抵抗で消費された静電エネルギーを求めます。
令和4年度上期の理論科目においては、難易度高めの問題であるように思います。
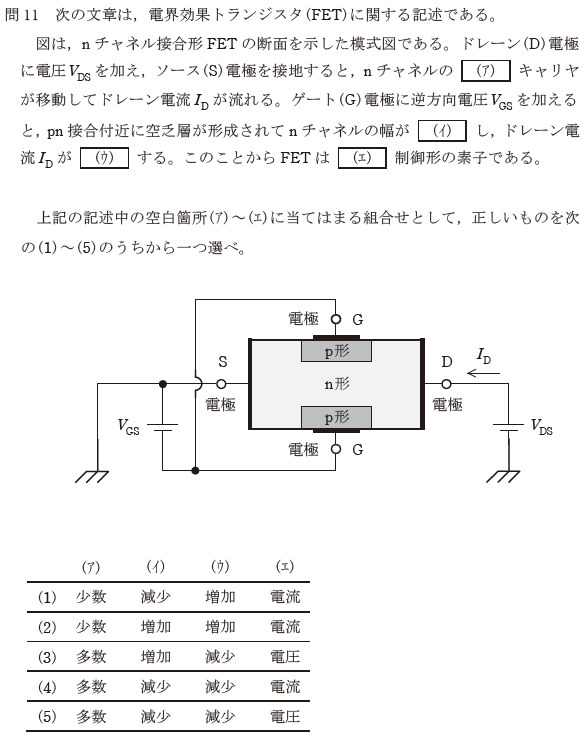
【正解の答え】問11:(5) 難易度:
私の結果 ⇒ 正解
【考え方】
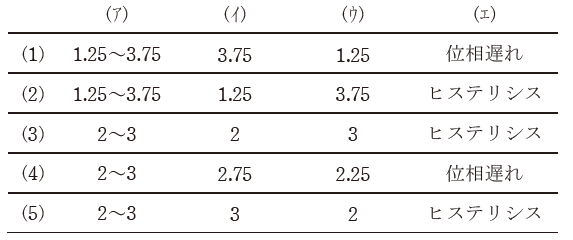
知識問題です。ダイオードの原理を知っていれば解けそうです。(エ)は難しそうですが、「電圧を制御することにより、Idの値をコントロールしている」のだから、「電圧」制御形が正解だろうな、ということで(5)を選択し正解でした。

【正解の答え】問12:(2) 難易度:
私の結果 ⇒ 正解
【考え方】
単位が[eV]なのがいやらしい問題ですが、「運動エネルギー[J]」=(1/2)×m[kg]v[m/s]^2)を知っていれば解けます。(2)を選択し正解でした。
ちなみに、電験王さんのサイトによると、「電子ボルト(エレクトロンボルト)とは、電子の電荷e[C]が真空中で1[V] をかけたときに加速されるときのエネルギーを1[eV]と定義した単位」とのことです。
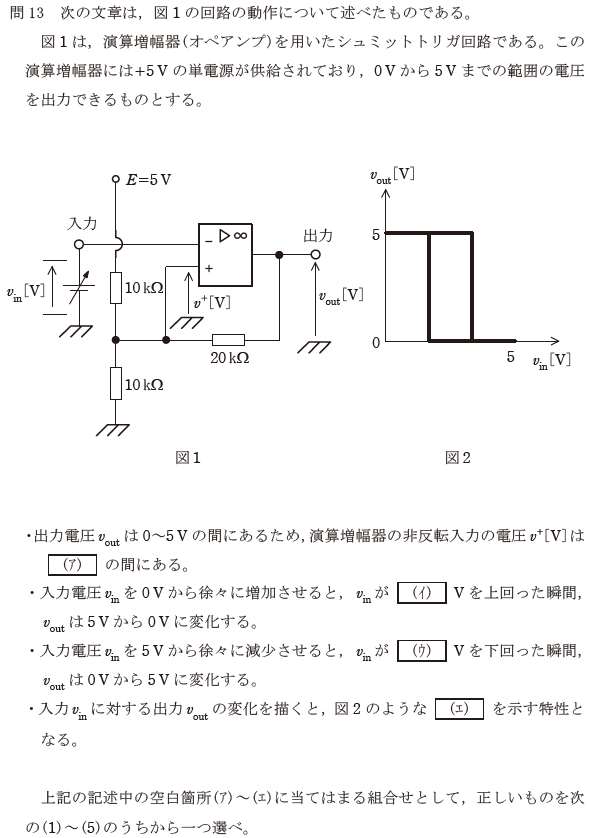
【正解の答え】問13:(5) 難易度:
私の結果 ⇒ 不正解(4)
【考え方】
まったく分かりませんでした。ただでさえ演算増幅器は苦手ですが、「シュミットトリガ回路」なんて聞いたことありません(忘れているだけかもしれませんが(汗))。苦し紛れに(4)を選択して不正解でした。
演算増幅器に流れる電流の向きを理解できれば、この問題を解くことができるようです。

【正解の答え】問14:(1) 難易度:
私の結果 ⇒ 正解
【考え方】
こ、これも分からん…。
(ア)「間接」だと意味が分からないし、「変位」では?
(ウ)これは「ホイーストンブリッジ」だろう。
これで(1)に絞れたので、(1)を選択したところ正解でした。
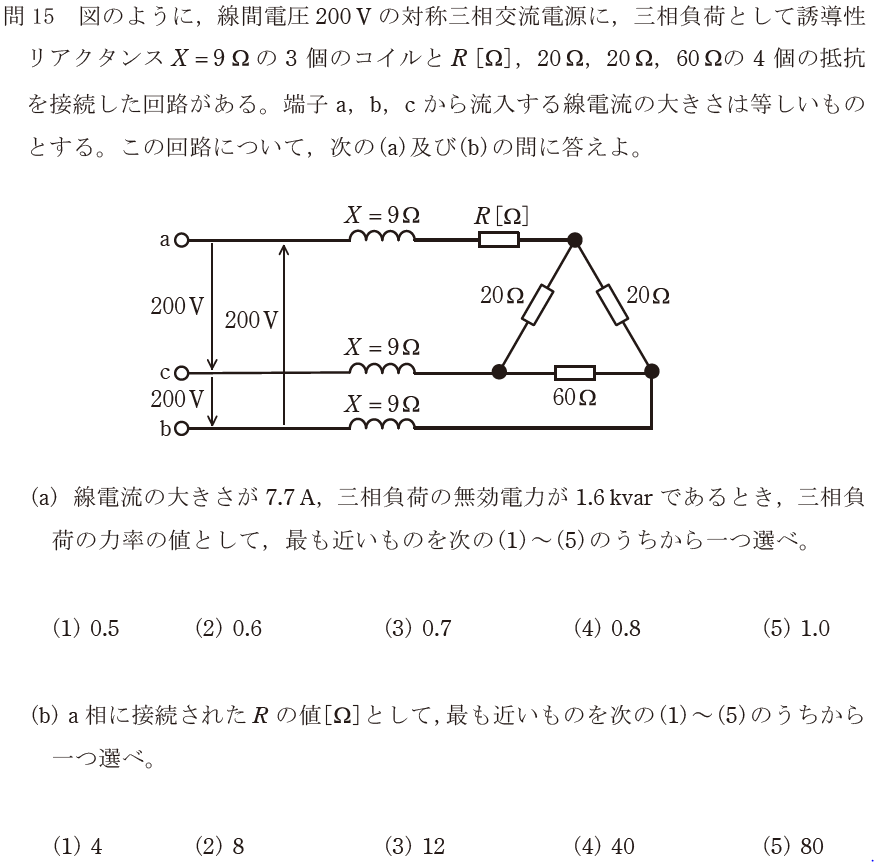
【正解の答え】問15(a):(4)、問15(b):(2)
私の結果 ⇒ (a)正解、(b)正解
【考え方(a)】 難易度:
条件よりsinθを求め、それからcosθを求めます。(4)を選択し正解でした。
【考え方(b)】 難易度:
(a)と比較して難易度が跳ね上がっている…。解き方が分からないから勘で解くしかない…。
cosθが「0.8」ということは、力率がそこそこ良いし、リアクタンスXの合計値に比べて、既に抵抗の合計値のウエイトは大きいので、抵抗Rの値は小さい値だろう。つまり、(1)4[Ω]か(2)8[Ω]だろう。計算問題において(1)と(5)は正解になり難い気がするので、(2)を選択したところ正解でした。
この問題を正攻法で解く場合、「Δ-Y変換」を駆使して各抵抗値を変換し、回路全体の有効電力を求め、それぞれの抵抗で消費される有効電力を求め、抵抗Rを計算する必要があります。
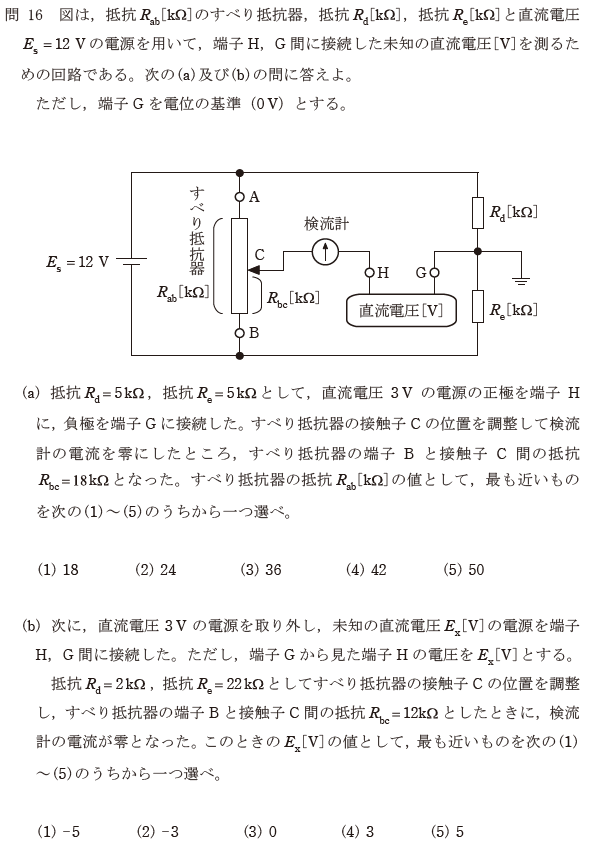
【正解の答え】問16(a):(2)、問16(b):(1)
私の結果 ⇒ 両方正解
【考え方(a)】 難易度:
見た瞬間に「ホイーストンブリッジ回路の問題だろうな」と推測できましたが、回路に直流電圧が引っ付いているのが厄介です。電験2種一次試験[理論科目]にて勉強した内容です。
検流形に電流を流さないために、回路の各ポイントの電圧の値を計算し、Rab[kΩ]を計算します。(2)を選択し正解でした。
【考え方(b)】 難易度:
こちらも(a)と同様の考え方です。(1)を選択し正解でした。
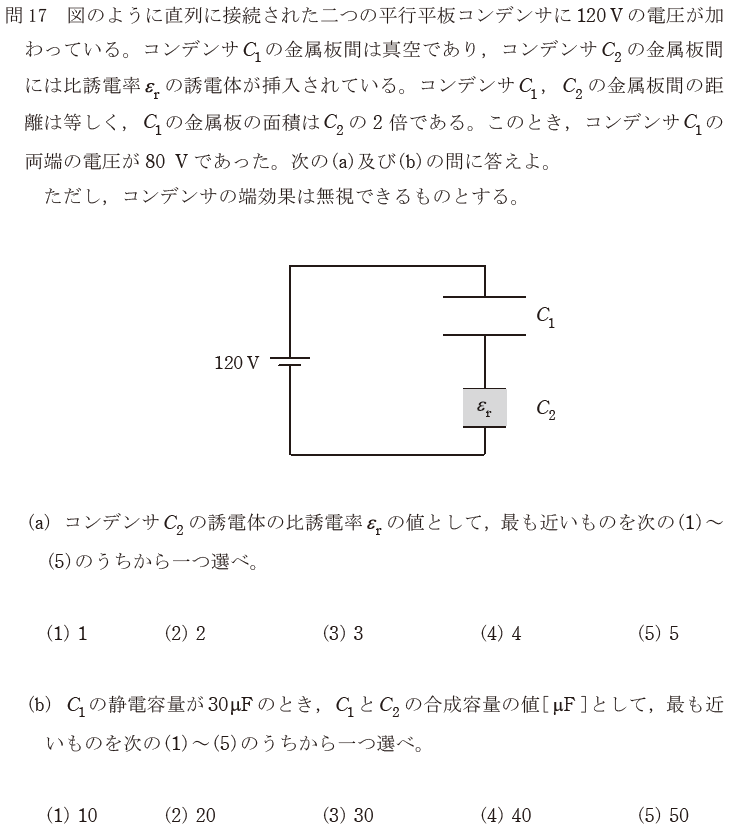
【正解の答え】問17(a):(4)、問17(b):(2)
私の結果 ⇒ 両方正解
【考え方(a)】 難易度:
特にヒネリもなく、公式を覚えていれば解けます。(4)を選択し正解でした。
【考え方(b)】 難易度:
こちらも公式を覚えていれば解けます。(2)を選択し正解でした。
(a)、(b)ともに、サービス問題だと思います。
解いてみての感想(4科目通して)
電験の勉強から9カ月程離れていましたが、かなりの好成績を収めることができました。
しかし、上記リンクから解いてみた軌跡を見ていただけると分かると思いますが、「非常に曖昧な知識で何となく正解している」という状況です。
おそらく、私以外の電験合格者の大多数も、このような感じではないでしょうか。(え、これだけテキトーなのは私だけ??)
なので、電験の勉強中の皆様には、「私のようにこれだけ適当でも合格点には手が届く」場合があるということを知っていただき、根気強く勉強を頑張って頂きたいです。分からないことでも勉強を続けていれば、そのうち分かるようになるし、結局わからないままのこともありますが、それでも合格は勝ち取れます。
いかがでしたでしょうか。
今後も、電験に関する記事を書いていきたいと思います。